[MachineLearning] 反向传播Back Propagation

反向传播的理解

知乎看到一个例子,的确有助于理解,摘抄整理下来.

如何直观地解释 back propagation 算法？ - 胡逸夫的回答 - 知乎

如图,我们尝试求$e=cd=(a+b)(b+1)$的偏导

假设现在要求$a=2,b=1$时的梯度,我们用偏导定义求出不同层偏导的关系

由链式求导法则:

$$\dfrac {\partial e}{\partial a}=\dfrac {\partial e}{\partial c} \cdot \dfrac {\partial c}{\partial a}$$ $$\dfrac{\partial e}{\partial b} = \dfrac{\partial e}{\partial c} \cdot \dfrac{\partial c}{\partial b} + \dfrac{\partial e}{\partial d} \cdot \dfrac{\partial d}{\partial b}$$

所以,从正向下层往上层看,

$\dfrac {\partial e}{\partial a}$ 等于$a\rightarrow c \rightarrow e$路径上偏导数的乘积.

$\dfrac {\partial e}{\partial b}$ 等于$b \rightarrow c \rightarrow e $ 和 $b \rightarrow d \rightarrow e$路径上偏导乘积的和

这里面就有一个问题:$c \rightarrow e$路径跑了两遍.如果面对更复杂的网络通路,这种重复的遍历会更多,必然会引起效率的下降.

所以BP就避免了这个问题,它使每个路径只访问一次就能求得顶点对所有下层节点的偏导值.

做法是:

从最上层节点开始,初始值为1,以层为单位处理.第一层$e$为1

到第二层,用1乘以到达下一层节点路径上的偏导值,结果存在这个节点.所以,$c = 1 2 = 2, d = 1 3 = 3$,即e对c的偏导值是2,e对d的偏导值是3.

第三层,$a = 2 1 = 2, b = 2 1 + 3 * 1 = 5$,即e对a的偏导值是2,e对b的偏导值是5

通过以上就可以对BP的工作原理有了一定了解.

再到神经网络中去看看BP算法:

Principles of training multi-layer neural network using backpropagation

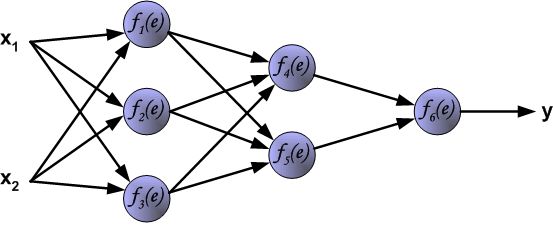
我们使用有两个输入,一个输出的三层神经网络:

注:从左到右三层分别是输入层,隐藏层和输出层

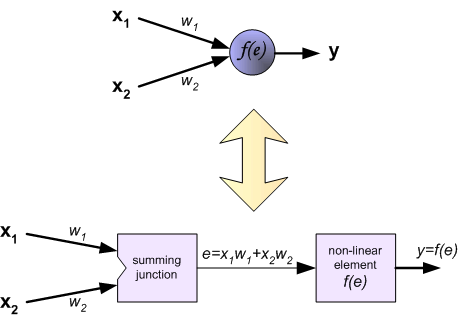
每一个神经元都包含两个单元:第一个单元负责合并权重系数和输入信号,第二个单元负责实现激活函数.信号e是第一个加法单元的输出信号,非线性函数y=f(e)是第二个单元的输出信号,y也是整个神经元的输出信号.

我们需要通过训练数据集去教神经网络.训练数据集包含输入信号(x1和x2),并且关联期望的正确输出z.网络训练是一个迭代过程.每次迭代中,权重都会根据新的训练数据变化.权重变化的算法如下:

每一次训练都从训练集的输入信号开始.经过这一阶段,我们能算出每一层每个神经元的输出值,如下图,$W_{x_{m}n}$表示第m个输入x到第n个神经元的权重,$y_{n}$表示第n个神经元的输出.

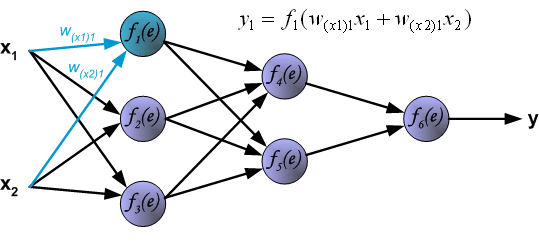
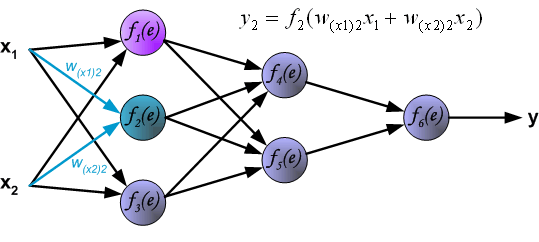
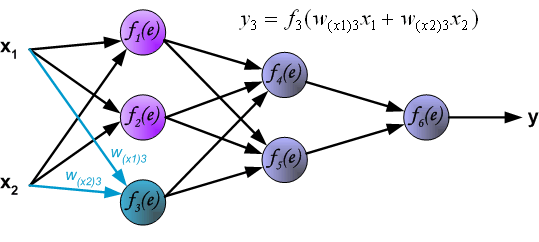
隐藏层的信号传播,Wmn是第m到第n个神经元的权重

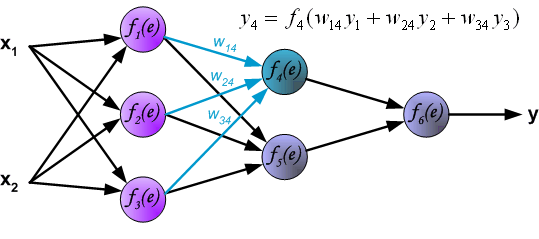
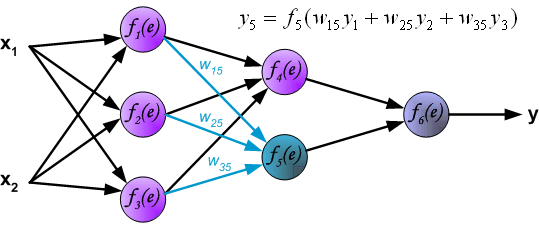
输出层的计算

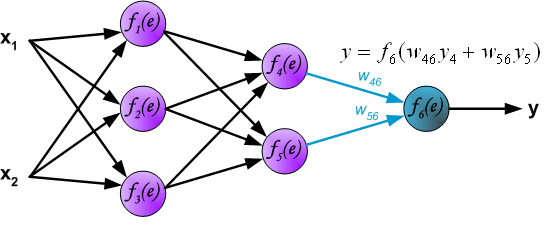
到这里就是前向传播.

下一步就是拿输出y和期望值z做比较,这个应该都比较熟悉了.比较的差别称为输出层神经元的错误信号d(感觉这个原文有点奇怪,反正我们的目的是降低y和z的差值)

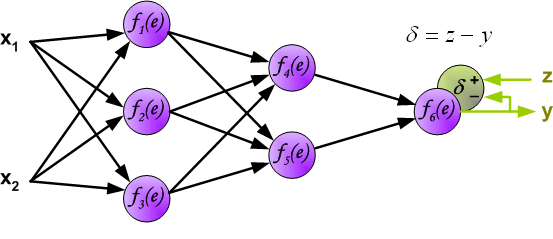
直接计算内部神经元的错误信号是不可能的,因为这些神经元的输出值是未知的.(知道为什么吗?)这时就要提到反向传播了,想法是,将错误信号d返回给所有神经元,输出信号是被讨论神经元的输入信号.

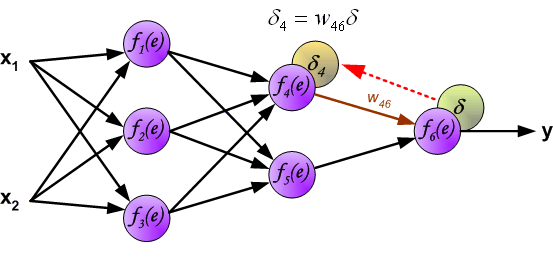
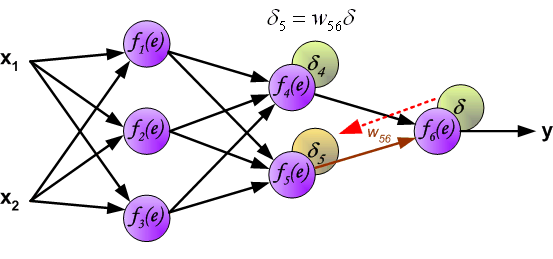
用于传播错误的权重系数$W_{mn}$等于在计算输出值期间使用的系数（就是反向计算的时候使用和之前一样的权重）。只是计算方向变了。对所有的网络层都按这个方式进行。

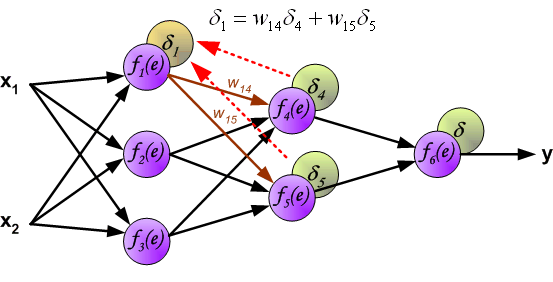
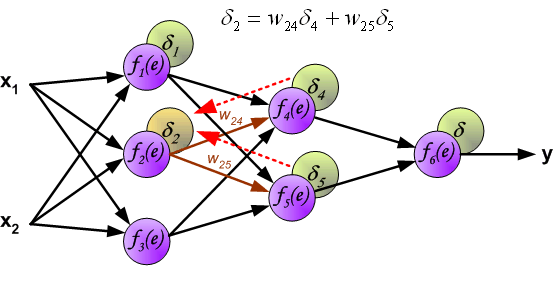
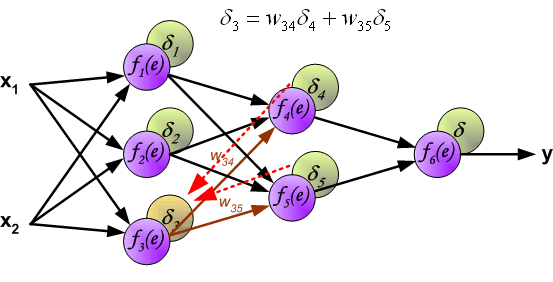
当所有神经元的错误信号都计算完毕后，每个神经元的计算权重按下图的方式更新。

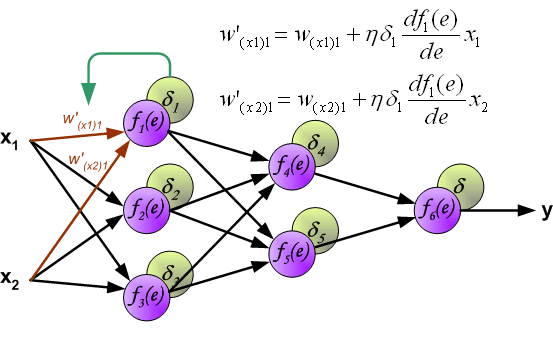
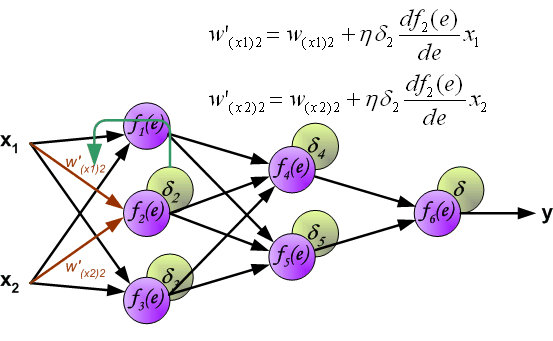
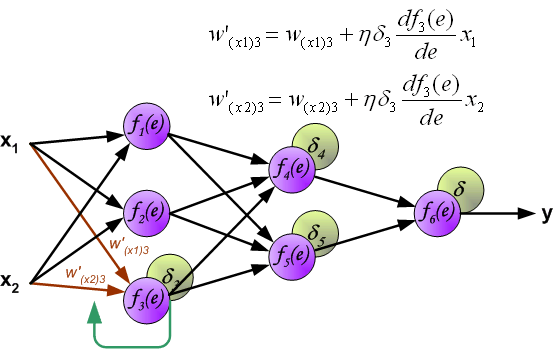
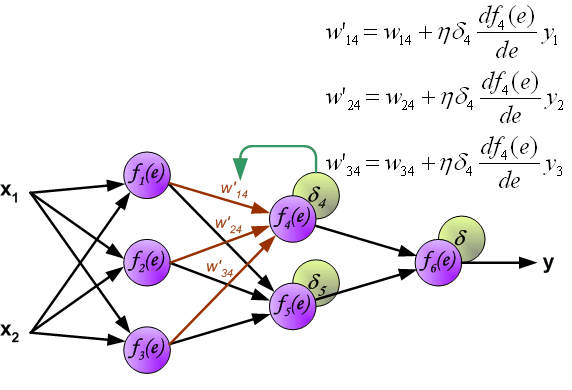
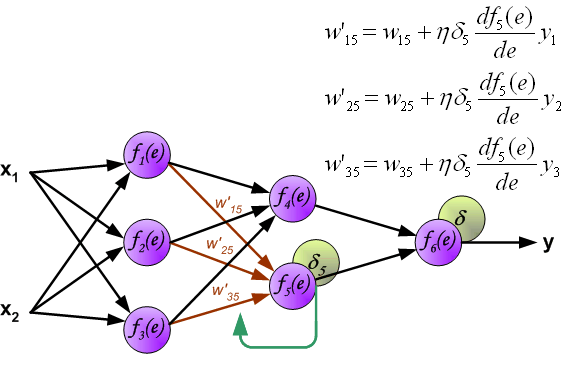
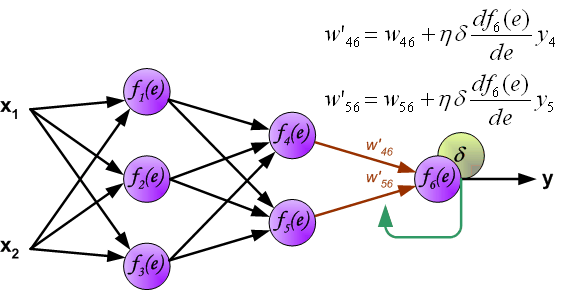
在更新W的时候方程右边会乘一个系数，这个系数就是学习率。详细介绍参见[MachineLearning] 超参数之LearningRate

有一篇通过代码介绍BP的文章也很推荐：

一文弄懂神经网络中的反向传播法——BackPropagation